# Machine Learning for Cities
# Introduction
Machine learning is the study of systems that improve their performance with experience (typically by learning from data)
- computer program should learn from experience like a human =- which would allow a computer to do a task based on prior experience, and do better each time.
Artificial intelligence is the science of automating complex behaviors that normally require human intelligence: vision, language understanding, learning problem solving, decision making, etc.
Data Mining is the process of extracting useful information from massive quantities of complex data
Linear Regression is a basic and commonly used type of predictive analysis. Does a set of predictor variables do a good job in predicting an outcome (dependent) variable? Which variables in particular are significant predictors of the outcome variable and how do they impact the outcome variable?
- can caluclate R2 value to see if the variables are correlated
- predict variable based on the f(x)
- large values imply positive correlation
- calculate a p value to justify the R2 value
Logistic Regression
- instead of fitting a line, logistic regression fits a s-shaped curve to the data. Conveying the probability of a given outcome.
- usually used for classification Classification predict a discrete value.
Regression estimate a numeric value.
Semi-supervised learning only some data points are labeled; the goal is still typically prediction
Active Learning Choose which data points to label; the goal is typically prediction
Reinforcement Learning Sequential actions with delayed rewards; goal is to learn optimal action in each state
Unsupervised Learning No labels, just input data x. Various goals including clustering, modelling, anomaly detection, etc.
Discrete y = classification
Continuous y = regression
# Decision Trees
- can do real value (regression)
- can do unknown category value (classification)
Learning a binary decision tree
- Start with all the data points in a single node. Predict the most common value.
- classification
- real mean value (regression)
- Choose the 'best' binary decision rule, and use it to split the data into two groups.
- Repeat step 2 on each group, until you run out of splits.
- when you run out of a given binary option, like if you do a split and you end up with 4 yes, and 0 bad, then the tree has no where else to go.
- Prune the tree to remove irrelevant rules. (helps avoid overfitting)
Choosing a decision rule
- if discrete: choose a class , split into = and !=
- if real: chose a threshold, split into > and <=
- to find threshold, sort the values and use midpoints
Information Gain is an information-theoretic measure of how well the split seperates the data
- it can be computed as a function of the numbers of + and - examples in each group
- the information gain is large when the proportions of positive examples in the two groups are very different, and zero when they are the same.
Pruning decision trees prevent overfitting
- if you do not prune decision trees, then they will predict every example perfectly
Decision Tree Advantages
- easy to learn the tree automatically from a dataset
- easy to predict the target value given the tree
- generally good classification performance
- can do both classification and regression and can use both real and discrete inputs.
- more important variables tend to be higher in the tree.
- Decision trees are interpretable
# Ensemble Methods
Ensembles are most useful when the predictors are maximally independent.
Stacking Simplest ensemble approach: learn a bunch of different models using the same training dataset, and let them vote or average the predictions.
Boosting Learn a sequence of classifiers, each focusing on examples where previous models had difficulty
- Adaboost: iteratively reweight the training data using the current set of models, giving expoenentially higher weight to incorrectl;y predicted data points and lower weight to correctly predicted points, then learn a new model using the reweighted data - finally do a weighted average of the individual predictions.
- has a learning rate
- Gradident boosting: on each step, fit the model to the residuals left by fitting all previous models. This is equivalent to gradient descene in function space.
- has a learning rate
Evaluating estimator performance
Learning the parameters of a prediction function and testing it on the same data is a methodological mistake: a model that would just repeat the labels of the samples that it has just seen would have a perfect score but would fail to predict anything useful on yet-unseen data. This situation is called overfitting. To avoid it, it is common practice when performing supervised machine learning to hold out part of the available data as a test set (X_test, y_test), then to learn a model on the remaining (training) data and evaluate its accuracy on the test data.
Advantages
- can start with weak classifiers and build to a stronger classifier
- reduces bias and not just variance
Disadvantages
- harder to implement
- less robust to outliers
- sensitive to parameter values
- not easily parallelizable
Bagging Bootstrap aggregation. learn a large set of models each using a different bootstrap sample from the training dataset. Final prediction is an unweighted average (or vote) of the individual predictors.
Advantages
- much higher performance than individual trees.
- increases stability and reduces overfitting
- trivial to implement and to parallelize
# Random Forests
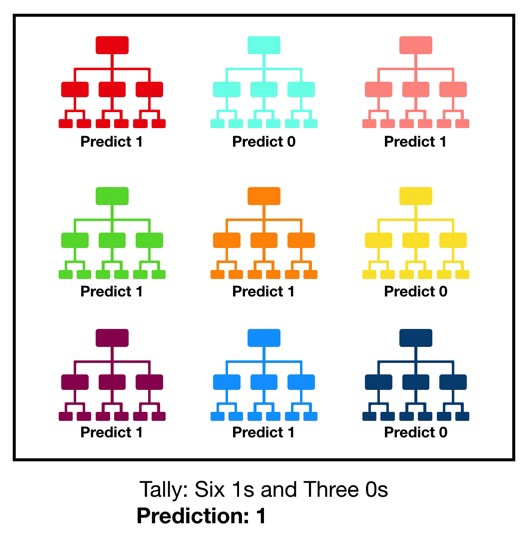
Random forest consists of a large number of individual decision trees that operate as an ensemble. Each individual tree in the random forest implements a class label prediction based on a sequence of condition checks and the class with the most votes becomes our model’s prediction. The fundamental concept behind random forest is a simple but powerful one - A large number of relatively uncorrelated models (trees) operating as a committee will outperform any of the individual constituent models. The low correlation between models is the key. Uncorrelated models can produce ensemble predictions that are more accurate than any of the individual predictions.
Put simply: random forest builds multiple decision trees and merges them together to get a more accurate and stable prediction.
One big advantage of random forest is that it can be used for both classification and regression problems, which form the majority of current machine learning systems.
# Decision trees
A decision tree is the building block of a random forest and is an intuitive model. It is a set of rules that can be learned from data and used to predict an unknown value. A decision tree is learned as follows:
- Start with all data points in a single node. Predict the most common value (classification) or mean value (regression).
- Choose the “best” binary decision rule, and use it to split the data into two groups.
- Repeat this for each non-terminal node of the tree, until some stopping criterion is reached.
The 'best' rule is based on calculating information gain. Information gain is an information- theoretic measure of how well the split separates the data. For regression tasks, we use the mean squared error criteria.
# Important hyperparameters
The hyperparameters in random forest are either used to increase the predictive power of the model or to make the model faster.
Firstly, there is the n_estimators hyperparameter, which is just the number of trees the algorithm builds before taking the maximum voting or taking the averages of predictions. In general, a higher number of trees increases the performance and makes the predictions more stable, but it also slows down the computation.
Another important hyperparameter is max_features, which is the maximum number of features random forest considers to split a node.
max_depth parameter is used to control the depths of trees in the model. More depth could lead to overfitting, so it is quite important to optimize this.
The detailed discussion on random forests and decision trees can be found here: https://towardsdatascience.com/understanding-random-forest-58381e0602d2
A super-useful variant of bagging. We learn a large set of models, like decisions trees, each using a different bootstrap sample from the training dataset. Final prediction is unweighted average (or vote) of the individual predictors.
- if original dataset has p dimensions, restrict to $\sqrt(p)$
- you get to chose number of trees in the forest
- change # of
- sample per leaf
- max depth
- min # of samples to split
- records and features to sample
Gini importance mean decrease in node impurity across all trees for splits on that variable
Advantages
- very accurate
- easy to use out of the box
- efficiently parallelizable
- not prone to overfitting
- can estimate feature importance
Disadvantages
- computationally expensive to train a model with N trees, m features, and n data points, complexity is O(Nm*n log(n)).
- Lots of memory to store trees
- Not very interpretable
# Support Vector Models
Support Vector Machines are optimization approach used primarily for binary classification, and are able to achieve high accuracy.
- decision boundary separates positive and negative training examples
- important to normalize values
- replace discrete valued attributes with dummy variables.
Margin how wide is the the area around a decision boundary in both directions.
- calculate by 2M / || w || or 2 / || w ||
Support Vectors points on the margin are called support vectors'
Maximum Margin Classifier - super sensitive to outliers, low bias to the data, but high variance. Meaning that it is fit to the training data, but can't handle any variance outside to the training data (overfitting the model)
Support vector classifier we use cross validation to determine, that a small percentage of misclassified data is okay in the long-run. This is accomplished by penalizing misclassifications to adjust the soft margin and move the support vectors.
Support Vector Machines
- the polynomial kernal programatically sets the polynomial function to different dimensiosn to find the best support vector classifier for the data.
- SVMs are not great fo r estimating probabilities
- relies on C (consequence variable which punishes wrong classification). If C is too large, then margin will be small.
- can be a black-box optimization model
# Bayesian Methods for Supervised, Semi-Supervised, and Unsupervised Learning
Semi Supervised learning only some data points are labelled; the goal is typically prediction
Unsupervised learning No labels, just input data x
# Naive Bayes (supervised)
We focus on classification, how likely is this data point to be in each class?
Conditional Probability P(x | y) what is the probability of x given y $$ f(x) = ((1/ (\sigma * (√2π))) * e ^ (-1/2 *((x - \mu)/\sigma)^2)) $$ Gaussian probability calculation
(1/ (standard deviation * (√2π))) * e ^(-1/2 *((x - mean)/standard deviation)^2)
when f(x = # | N(sample mean, sample standard deviation))
- can only do classification not regression
- we assume conditional independence
- if assumption is true, then logistic regression and naive bayes models will converge to the same values, but NB converges quicker for smaller amounts of data.
# Semi-supervised
Expectation-Maximization (EM) moves back and forth between two probabilistic algorithm.
- we assume uniformity since we don't know the priors from unlabelled data.
# Clustering
- Clustering provides a useful summary of a large dataset, representing the N data records using only k << N clusters.
- Helps understand the underlying structure of the data.
- help detect anomalies, by finding points that are outside a given cluster.
# K-means clustering
Assume that all attributes are real-values, and we compute the centroid or mean value of each cluster. This is the sum of squared errors for each data point. assuming that each x is mapped to the closest cluster center.
- define the number of clusters
- each data point finds which cluster centroid it is closest to.
- repeat until convergence!
- K means will eventually converge to a solution where each data cluster is grouped.
- It will not however always find the optimal solution.
- we run into local optima - where it gets good at looking at the training set, but cannot cluster new unseen data points.
- We can run the model multiple times to avoid this with different start states and clusters
- Choose the k (# of clsuters) that minimizes a measure of distortian with a penalty for more complex models.
- It will not however always find the optimal solution.
- It halts creating and optimizing clusters when either:
- The centroids have stabilized — there is no change in their values because the clustering has been successful.
- The defined number of iterations has been achieved.
# Leader Clustering
We take a small subset of representative points and group each incoming data based on the initial leaders of the set.
Higher the AUC, better the model is at predicting 0s as 0s and 1s as 1s.
# Bayesian Networks and Causality
3/26/2020
What to study for midterm
Why are Bayes Nets so useful?
- interpretable structure
- represent a compact distribution and infrences
Multiply each probability by the given variable
How to build a Bayes Net
- choose relavent variables
- chose a casual ordering
- if xi influences xj, then order them appropriately
- Environmental variables are going to be first in the ordering
- observational variables are generally last
- The ordering is top --> down
- Add links must be acyclic
- each edge has a direction
- acyclic means not allowed to have feedback loops ****- everything must end
How to interpret Bayes Net Structure?
- Given parent value creates a conditionally dependent
D-seperation
- think about the relationships between tow variables figuring out if they are conditionally independent
- are the variables blocked?
- what doese it mean for a path to be blocked?
- does a value remain static or dynamic based on influence of another upstream variable.
- common effect instead of a common cause the roles are reversed
Probabilistic inference?
- given what we know about the other variables
Joint prbabilities
Approximate Inference
- sample parent before sampling child
- randomly chose proability for joint distributions
Bayes Net Parameter learning
- learn probability based on parent values, by doing maximum likelyhood
Bayes net structure search
which structure captures the data best? There are many possibilities in determining which structures are best.
hill-climbing- make one change at a time to improve the overal quality increases the score until you find a dead-end. Always going to make a move that improves the score
simulated-annealing -when you select a move at random, if it improves the score you always make it, we sometimes make it even if it decreases the score, you gradually decrease the probability of making a move that decrease the score over time - which transforms into hill-climbing.
- can help get you out of local optimum
How to score a structure?
What moveset to use?
- add an edge
- remove an edge
- swap attributes
How to score?
- we would have to score every single structure we create to evaluate each structure by computing maximum likelihood, then compute the log-likelihood of the training dataset given the structure and parameters.
score = log likelihood - constant * number of probabilitis in all the conditioanl tables
k = total number of parameters
causal partial ordering
k2 - is a causal partial ordering using domain knowledge to sort ordering of the network.
Causal Bayesian Network CBN
Markov Condition given its parents (causes), each variable is conditionally independent of its non-descendents.
- force to take on a value called an interventaion
- some edges may be directed, some undirected
How can we ever get a directed edge?
- Answer V-structures or colliders
PC algorithim - causal algorithim created in the philosophy department
- start with a complete undirected graph
- identify v-structures and remove and independent edges
- avoid creating directed cycles and additional V-structures
Causal Markov: a variable is proabilisitically independent of its non-descendeants (non-effects) conditional on its direct causes.
- permits inference from dependence to causal connection.
Causal Fathfulness: two variables are not going to conditional independence by accident.
- if two variables are conditionally independent then causal seperation
Causal Sufficiency: no unmeasured common causes
Fast Causal Inference
- not that fast, not that scalable
- rather than a causal graph it learns and ancestral graph, when we have a direct edge, it says there may be some hidden causes between two variables.
Causal orientation methods Gaussian. : being or having the shape of a normal curve or a normal distribution.
additive nosie - noise can be gausian or non-gausian
Bayes Nets
Bayes Nets provide a useful graphical represenation of the probabilisitc + causal relationships between variables, gives nice model of the dataset.
Useful for prediction
Useful for anomaly detection - once you learn the model and dataset, you can visualize any variable that sits outside the net.
Provides a compact structure which enables us to efficeintly compute probability distributions for any unobserved variables given observations of other variables.
Exam at 10:00 - submit by 11:35am not late work accepted.
MLC Midterm prep
# Review Lectures
Take notes on each lecture and review the lab
- [x] Introduction to Machine Learning
- [x] Lab 1
- [x] Binary Decision Trees
- [x] Lab 2
- [x] Ensemble Models
- [x] Lab 3
- [x] Support Vector Models
- [x] Lab 4
- [x] Naive Bayes Theorem
- [x] Lab 5
- [x] Clustering Methods
- [x] Lab 6
- [x] Practice Problem Review
# Midterm Answer Review
# Gaussian Processes for Modeling and Prediction with Dependent Data
4/16/2020
Most urban problems are not independent of one another. They all affect one another in some upstream or downstream fashion.
First law of geography: Everything is related to everything else, but nearby things are more related than more distant things.
Kernal regression estimate the distance between points and time. (space-matters!)
- kr, does not have any underlying probabilistic model of the data. We have a best guess ot the data, we have the mean of the distribution.
- we can't reason variability or risk.
- we can't reason joint possibilities.
Gaussian Process (GPs) are approach for supervised learning with dependent data.
- regression
- classification
- good at change detection
GPs are a function approximator,we learn $y= f(x)$ from a set of (xi , yi)
- non-linear flexibility to fit very complex functions
- $#$ of parameters increases with $#$ of data points.
- Bayesian assume a prior distribution over functions $f(x)$.
Univariate Gaussian Distribution distribution over scales (real #s)
Multivariate Gaussian Distribution distribution over vectors.
Gaussian process distribution over functions, an infinite-dimensional vectors on a real-number line.
- we assume each real number has a possible y relating x to y.
stochastic process is a collection of random variables, ${f(x): x \epsilon X}$
Two free parameters, kernel bandwidth $\tau$ and noise variance $\sigma^2$
Noise Variance If $\sigma^2 == 0$ , this means that we will learn a function that will pass through every single data point. Commonly $\sigma^2 > 0$
optimize the marginal likelihood of the training data.
# Anomaly and Outlier Detection
04/23/2020
Treat anomaly detection as a binary classification problem, identifying each record as anomalous or normal.
model based anomaly detection
make the model as accurate as possible, given the normal model.
Define what it means to have a row as anomalous?
Distance-Based Anomaly Detection
- choose a threshold and detect outside of that
- set x signifier for the anomaly.
cluster-based anomaly detection
- learn the mean for each cluster
- learn the covariance for each cluster
- uses a metric that takes cluster into account
if your normal class has underlying structure this is helpful.
70% training 30% testing
join the svi dataset writing in paper
how many total rows are we using 30*2
how long did it take to train each model? computational model
highest was boosting was SVM about 30 -40 minutes
we evaluate on the recall, precision, accuracy, latenecy
31089 features
def love(amount):
amount += 1
return amount
amount_of_love = 0
while amount_of_love < 100:
amount_of_love = love(amount_of_love)
print(amount_of_love)