Applied Urban Science

Timeseries

Goals for a timeseries analysis

• pattern recognition
  • signal detection, trends, weekly/monthly patterns, annomaly detection etc
• predictive modelling
  • stock prices prediction, weather forecast etc

Understanding trends

You can compare the value at the end of the interval an beginning and subtract from one another and divide by the length of the interval to get a rate of decline/increase.

Linear Regression

linear regression is a linear approach to modelling the relationship between a scalar response and one or more explanatory variables.

statsmodel.OLS()

TIP

R-Squared value shows how much of the data can be shown as a function of the regression

Rolling Averages

Can smooth out a noisy dataset by taking a yearly average, or 7 year average by looking at the data in sets of windows. Instead of daily or monthly data points to look at the overall trend.

Seasonality

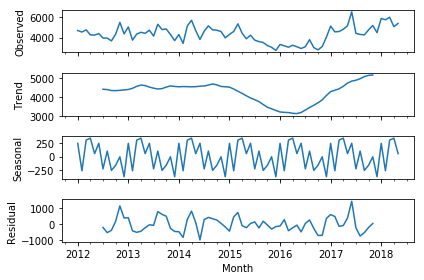
Trends are continuous increases or decreases in a metric's value. Seasonality, on the other hand, reflects periodic (cyclical) patterns that occur in a system, usually rising above a baseline and then decreasing again.

Periodiatic functions with consistant set(s) of period(s). Finding seasonality can be difficult based on deciding which period to look at, every Monday, or weekly, or weekday etc? There are usually multiple periods to consider when doing analysis.

TIP

52 weeks in a year

When using statsmodel.seasonal_decompose()

additive or multiplicative

Additive = y(t) = Level + Trend + Seasonality + Noise

Multiplicative = y(t) = Level * Trend * Seasonality * Noise

If the seasonality and residual components are independent of the trend, then you have an additive series. If the seasonality and residual components are in fact dependent, meaning they fluctuate on trend, then you have a multiplicative series.

we use multiplicative models when the magnitude of the seasonal pattern in the data depends on the magnitude of the data. On other hand, in the additive model, the magnitude of seasonality does not change in relation to time.

Additive model is used when the variance of the time series doesn't change over different values of the time series. On the other hand, if the variance is higher when the time series is higher then it often means we should use a multiplicative models.

What is Residual

not explained by seasonability or trends - so pulled out as the leftovers.

Periodogram

Plots the relative strength of the period as the function the frequnecy.

Autocorrelation

Measures the correlation over a set period of time.

• Autocorrelation represents the degree of similarity between a given time series and a lagged version of itself over successive time intervals.
• Autocorrelation measures the relationship between a variable's current value and its past values.
• An autocorrelation of +1 represents a perfect positive correlation, while an autocorrelation of negative 1 represents a perfect negative correlation.
• Technical analysts can use autocorrelation to see how much of an impact past prices for a security have on its future price.

Probabilistic Time-series model

random variables are independent of each random variable.

TIP

Efficient Market

Market efficiency refers to how well current prices reflect all available, relevant information about the actual value of the underlying assets. A truly efficient market eliminates the possibility of beating the market, because any information available to any trader is already incorporated into the market price.

Random walk

non stationary

In each time period, going from left to right, the value of the variable takes an independent random step up or down, a so-called random walk. If up and down movements are equally likely at each intersection, then every possible left-to-right path through the grid is equally likely.

TIP

Head + Shoulder pattern is a chart formation that appears as a baseline with three peaks, the outside two are close in height and the middle is highest

TIP

In mathematics, a Markov decision process (MDP) is a discrete-time stochastic control process. It provides a mathematical framework for modeling decision making in situations where outcomes are partly random and partly under the control of a decision maker.

TIP

The Martingale property states that the future expectation of a stochastic process is equal to the current value, given all known information about the prior events.

The problem is as follows: Consider a town consisting of 3x2 blocks shown below. A drunken sailor stands in one of the two crossroads and he wants to leave the town. Since the sailor is very drunk, the probabilities of travelling up, down, left or right are equal.

WARNING

• What is the blue region on autocorrelation - acts like confidence intervals. What can be observed from white noise
• Why does taking the log change the graph?

ARMA ( auto correlation and moving average )

WARNING

stationary model

if you see the model is not stationary, you need to applying differencing.

White Noise

When the data hovers around the normal distribution. If you add white noise to the linear trend model, you can get a steady trend with fluctuations.

Stationarity

We model the random variables x(t) describing the distributions - acknowledge the variables are related we describe the joint distributions.

• described by the variance of standard deviations.
• only depends on the lag
• function of the single variable - the lag.
• the expected value of the timeseries does not change over time.
• the average does not change over time

WARNING

no trend exists when the dataset is stationarity. no trend does not mean stationarity.

The fact that you change the observation x steps ahead, then time is not a variable since the correlation is the same.

function of the lag not time.

In the most intuitive sense, stationarity means that the statistical properties of a process generating a time series do not change over time . It does not mean that the series does not change over time, just that the way it changes does not itself change over time.

https://stats.stackexchange.com/questions/396522/moving-average-process-stationarity

TIP

low p-value of Add-Fuller tests suggests no differencing is needed. check with the value of significance $/alpha$

MAp Model

Moving Average Process

weighted average of random average, which sum to 0. This means that the model is stationary.

AR

Auto Regressive

Previous observation

Arma Model

Autoregression + moving average

stationary

Don't apply if timeseries is non-stationary. First make the dataset stationary then apply ARMA. Applying differencing to get the observation today vs yesterday to smooth or create stationarity.*

ARMIA Model

Auto Regressive Integration Moving Average

Good for descriptive analysis - tells you what can be explained by auto correlations and for anomaly detection. What can you learn about today that can't be explained by historical dataset?

AR: Autoregression. A model that uses the dependent relationship between an observation and some number of lagged observations.

I: Integrated. The use of differencing of raw observations (e.g. subtracting an observation from an observation at the previous time step) in order to make the time series stationary.

MA: Moving Average. A model that uses the dependency between an observation and a residual error from a moving average model applied to lagged observations. Each of these components are explicitly specified in the model as a parameter. A standard notation is used of ARIMA(p,d,q) where the parameters are substituted with integer values to quickly indicate the specific ARIMA model being used.

The parameters of the ARIMA model are defined as follows:

d: The number of times that the raw observations are differenced, also called the degree of differencing.

p: The size of the moving average window, or the number of the moving average terms, also called the order of moving average.

q: The number of AR terms included in the model, also called the lag order.

TIP

Use one moving average and multiple auto regressive models for a given set.

The more you difference, the more stationary you make the model. You need to have some auto-regressive variables to model.

WARNING

If lag 2 or lag 3 etc are significant and not lag 1 then it is an unnatural to model when differencing.

Dimensionality Reduction

When the dimensionality 𝑛 of the feature space (number of regressors) is too high with respect to the number of observations, it may cause multiple issues:

complexity: the model involving multiple regressors becomes difficult to fit and interpret;

multicollinearity: a large set of regressors could encounter substantial correlations, leading to multicollinearity of regressors and high variance in their estimates, making coefficients hard to interpret/rely on;

overfitting: as multiple regressors might contain a lot of relevant but also irrelevant information, the model could pick it up, becoming too specifically adjusted to the training set, which would reduce its generalizeability (performance over the validation/test set);

Feature selection aims to reduce dimensionality of 𝑥 by removing some of its components 𝑥𝑗 which turn out to be the least relevant for the model, i.e. have the lowest positive or even negative impact on the model performance over the external validation set. This way feature selection provides a mapping of vectors 𝑥 into a shorter vector of its subcomponents, e.g.

(𝑥1,𝑥2,𝑥3,𝑥4,𝑥5)→(𝑥1,𝑥3,𝑥5).

Principal Component Analysis

You don't want to rely on the leading principal to be the deciding factor for output information. Since the leading component may not represent the variance of the entire dataset.

Each component is orthoganal to the original dataset, thus independent which removes the issue of multicollinearity.

Allows you to work with initially unrelated data to become related.

TIP

Transforming Feature Space

rotate the data! Helps remove implicit ties between the observations. Removes correlations, which means the features become independent.

Also helps you see which feature contributes to the feature location, by looking at hte leading axis after rotation.

WARNING

Make sure to scale/standardize the data before applying PCA.

Leading PC - uncorrelated low-dimensional features space

• data exploration
• modelling

Limitations

• relevance
• interoperability
• linear

WARNING

PCA can only account for linear correlations in the dataset.

limitation

Hardly interpretable - they are expressed as linear combinations of the original observation. The coefficient, are somewhat arbitrary.

Pareto Rule

20% of the information often provides 80% of the value.

Non Linear Dimensionality

Reduce the dimensionality while maintaining the patterns in the data.

PCA

WARNING

Train the PCA using only training data, don't use test data.

Gaussian Kernal

Essentially takes the distance between two points and takes the exponent.

Dask

dask

Dask is popularly known as a ‘parallel computing’ python library that has been designed to run across multiple systems. Dask can efficiently perform parallel computations on a single machine using multi-core CPUs. For example, if you have a quad core processor, Dask can effectively use all 4 cores of your system simultaneously for processing. In order to use lesser memory during computations, Dask keeps the complete data on the disk, and uses chunks of data (smaller parts, rather than the whole data) from the disk for processing. During the processing, the intermediate values generated (if any) are discarded as soon as possible, to save the memory consumption.

Common uses:

Dask DataFrame is used in situations where Pandas is commonly needed, usually when Pandas fails due to data size or computation speed.

1. Manipulating large datasets, even when those datasets don’t fit in memory
2. Accelerating long computations by using many cores
3. Distributed computing on large datasets with standard Pandas operations like groupby, join, and time series computations

The APIs offered by the Dask dataframe are very similar in syntax to that of the pandas dataframe.